Get Started

General Context

The HCS Toolbox supports an model-based control systems design under the conventional framework presented at Fig. 1.1:

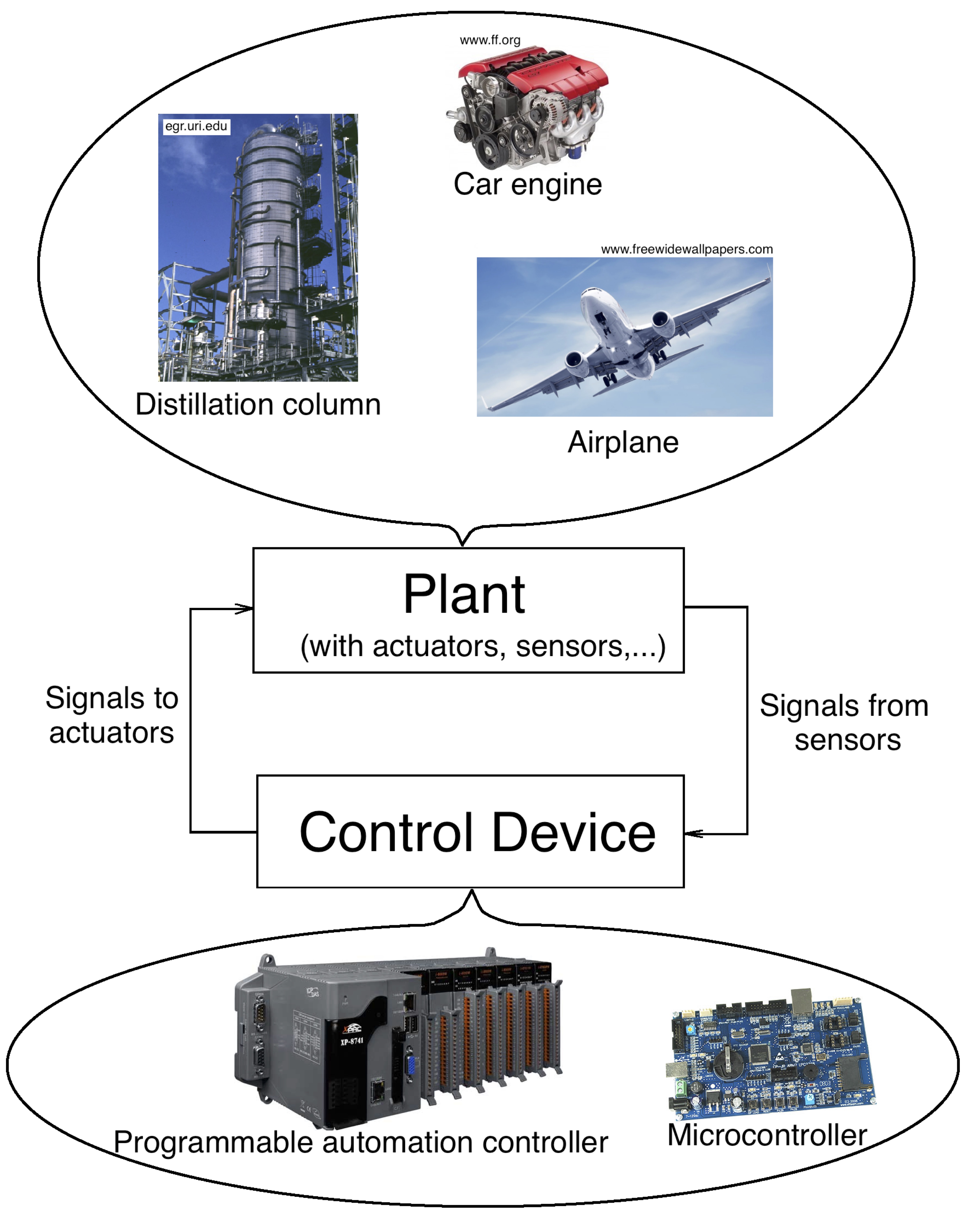
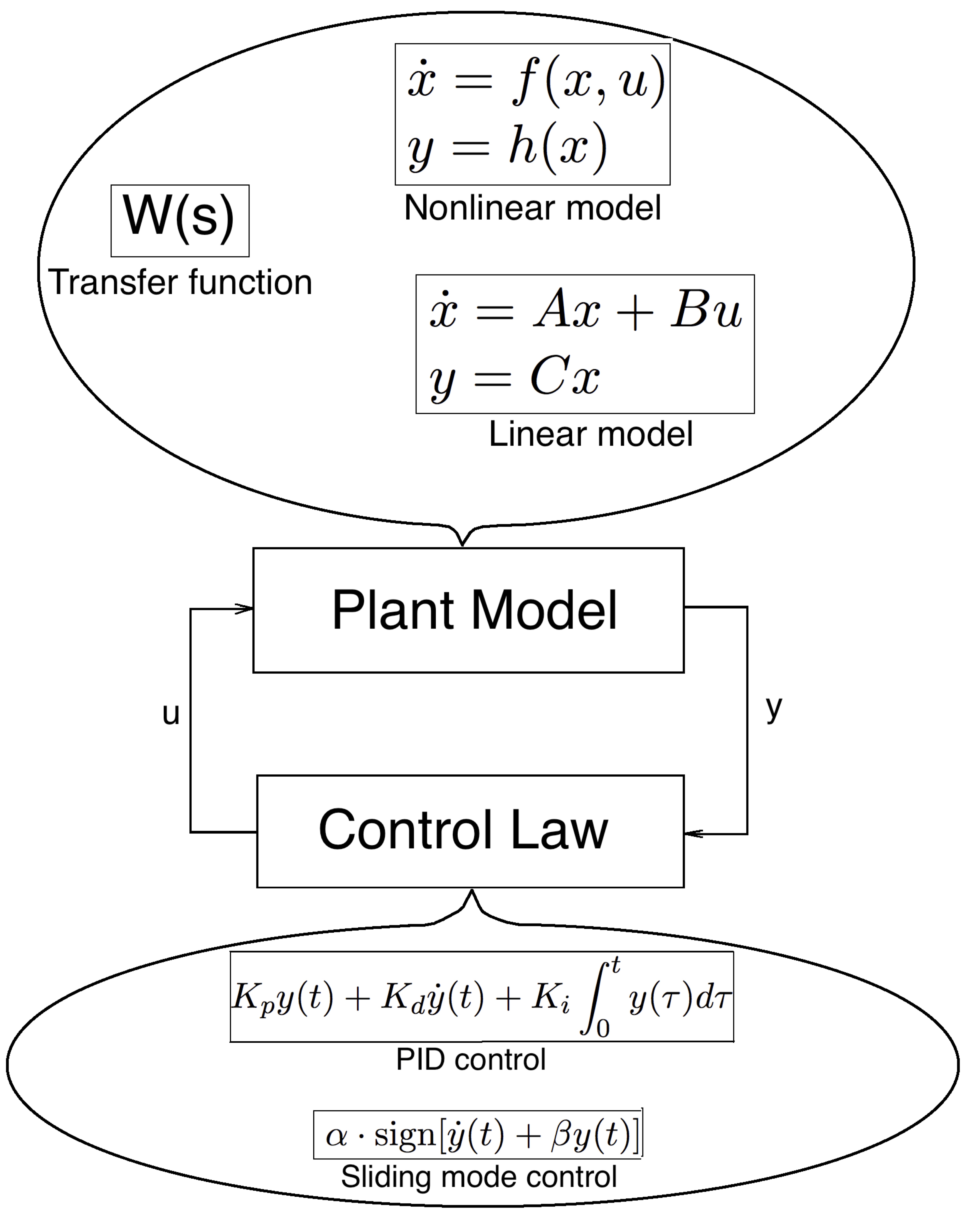
Figure 1.1: Model-based control systems design

where $x\in\mathbb{R}^n$ - the system state, $u\in \mathbb{R}^m$ - the control input , $y\in \mathbb{R}^k$ - the system output, the matrices $A\in \mathbb{R}^{n\times n}$, $B\in \mathbb{R}^{n\times m}$ and $C\in \mathbb{R}^{k\times n}$ are assumed to be known.

$$ $$

Conrtol problems which can be solved using HCS toolbox

design of a state feedback law $u$ for robust finite/ fixed-time stabilization of the state or the output (i.e., $y(t)=\mathbf{ 0}, \forall t \geq T$)

upgranding a linaer stabilizing controller (e.g.; $u=K_{ lin } y$) to a nonlinear one with a better quality

design of a dynamic obserever for finite/fixed-time estimation of the state $x$ based on the measured output $y$

upgrading a linear (Lunberger) observer of $x$ to a nonlinear one with a better quality

design og an observer-based feebbach law for robust finite/fixed-time stabilization of the system state to zero using the output measurements only

$$ $$

The HCS toolbox solves the above design problems based on the concept of the $\textbf{generalized homogeneity}$

$\texttt{m-functions}$- for homogeneous controllers/observers design
$\texttt{m-functions}$ for discretization of controllers/observers
examples of homogeneous systems design realized in $\texttt{m-files} $
demo of upgrading linear controller/observer for the rotary inverted pendulum to homogeneus one with a better quality.
various $\texttt{m-functions}$ for homogeneous systems

$$ $$