Variable Resolution Discretization
in Optimal Control
Remi
Munos
Andrew Moore
Introductive papers:
Variable
Resolution Discretization in Optimal Control.
Machine Learning Journal, 2002. Postscript
(431KB).
Variable
resolution discretization for high-accuracy solutions of optimal control
problem.
International Joint Conference on Artificial Intelligence
1999. Postscript
(315KB).
Influence
and Variance of a Markov Chain :
Application to Adaptive Discretization in Optimal
Control.
IEEE Conference on Decision and Control 1999. Postscript
(180KB).
Description of the optimal control problems:
A few videos:
Description of the method :
Introduction :
-
We consider a continuous time & space
control problem (see the paper: A Study of Reinforcement Learning in
the Continuous Case by the Means of Viscosity Solutions, Machine Learning
Journal. Postscript
(171KB)).
-
We assume that we have a model of the state dynamics and the reinforcement
functions.
-
The goal : find the optimal controller.
-
Method used : discretization techniques
-
Problem : Curse of dimensionality
-
Thus we consider variable resolution discretizations
-
We consider the "General towards specific" approach
-
Thus our concern is where to increase the resolution of the discretization.
1- The discretization process
-
We discretize the continuous process by using a structure based on a kd-tree,
for which the splitting is done in the middle of the cells ina direction
parallel to the axes.
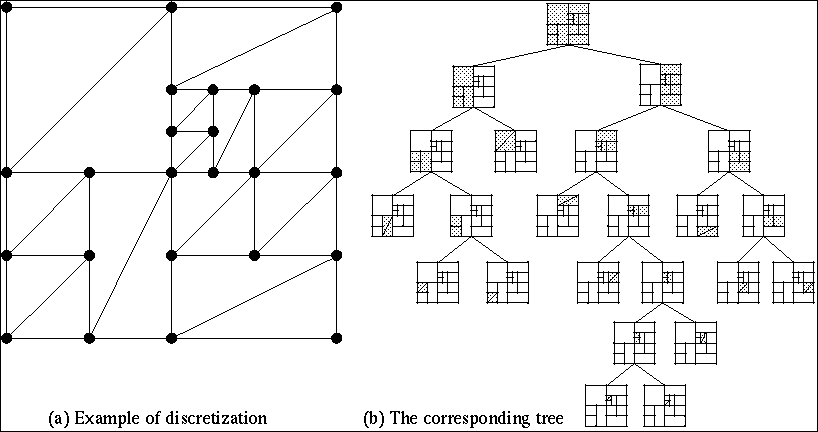
-
On each leaf of the tree (cell) we implement a Kuhn triangulation, so that
the function approximated is linear inside each triangle.
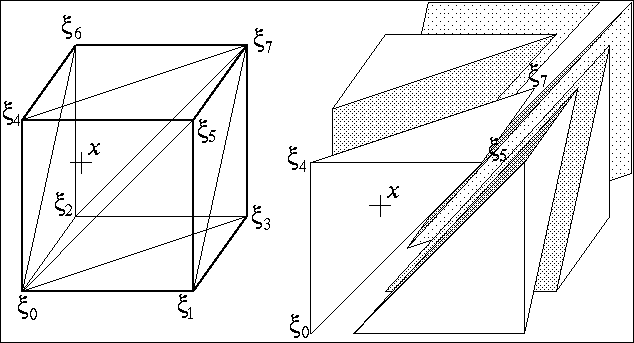
-
We assign a value at each corner.
-
The values required to satisfy a Dynamic Programming equation : the value
at a corner (xi) is the sup of the discounted value at the iterated point
(eta).
-
Since the function is linear is the triangle containing eta, the value
at that point can be expressed as a linear combination of the values at
the corners (xi_i) weighted by some coefficients (called the barycentric
coordinates) that are positive and sum to one.
-
Thus doing this interpolation is mathematically equivalent to defining
a Markov Decision Process whose probabilities of transition from xi to
xi_i are these barycentric coordinates.
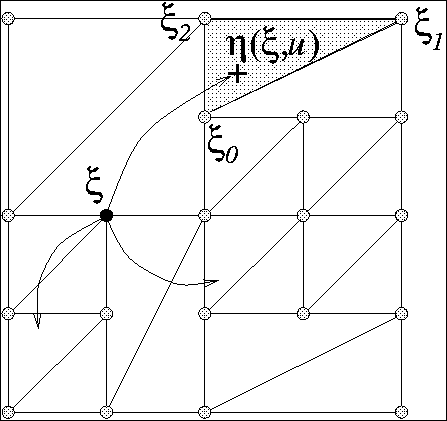
-
For a given discretization, we build the corresponding MDP, we solve it,
and now, based on the approximated values obtained at the corners, we decide
where to increase locally the resolution in order to improve the approximation
of the value function and the optimal policy. Thus we build a new discretization
and start again.

-
Now we'll explore different splitting methods and compare the resulting
discretizations obtained.
-
But first, here is a description of a simple 2-dimensional control problem
used in our simulations.
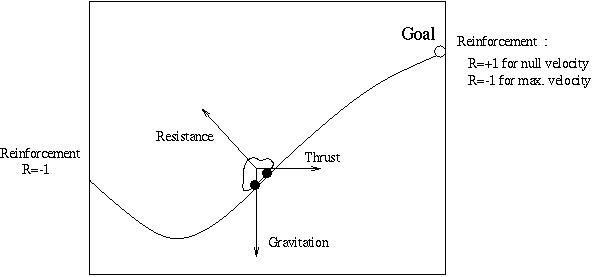
2- Description of the "Car
on the Hill" control problem
-
It's a car running on a hill. It's defined by its position and velocity
and controlled by a discrete positive or negative constant thrust.
-
See hillcar.html
for an C implementation of the state dynamics.
-
Here we consider deterministic state dynamics.
-
The reinforcement is the following :
-
No intermediate reinforcement
-
There is a punishment (R=-1) if the car exists from the left
-
There is a reward (R=+1) if the car reaches the top of the hill with a
zero velocity. If it reaches the top of the hill with a positive velocity,
it is punished by a cost linear with the terminal velocity.
-
Thus the goal is to reach the top of the hill as fast as possible with
a terminal velocity as low as possible.
-
Here is the Value function V of this problem (computed by a regular grid
of 256x256).

-
We notice that there is a discontinuity frontier (1) in V and 2 discontinuity
frontiers (2 and 3) in the gradient of V.

-
We run a couple of optimal (related to the current approximation of V)
trajectories:
-
And here is the switching boundaries in the optimal control:










