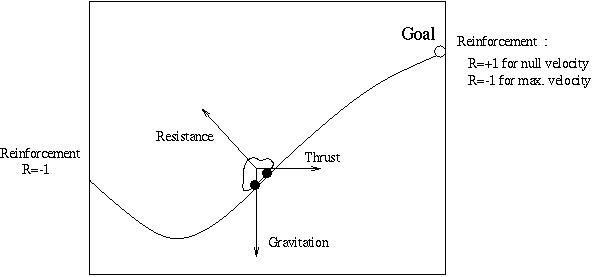
Description of the task : ``Car on the Hill''


 

The state space :

The car is defined by the 2-dimensional state x=(y,v)
where y is its position and v its velocity.
The control space :
The control u is a 1-dimensional variable that takes a
finite number of possible values between u_min and u_max.
It represents the thrust applied to the car.
The state dynamics :
The state dynamics is defined by the differential equation :
dx
-- = f(x,u)
dt
in the deterministic case, and by the stochastic diff. eq. :

dx = f(x,u) dt + s(x,u) dw

in the stochastic case. Here dw is a Wiener process.
(The formulation of the stochasticity is explained is the
function hillcar_noise).

The reinforcement functions :
The current and terminal reinforcement functions are described
in the functions :
Code in C :
 

/* Definition of some constants and basic functions */
#define A 1.0
#define B 5.0
#define C 0.0
#define MASS 1.0
#define GRAVITY 9.81
#define f1(x) ((x) * ((x) + 1.0))
#define f1_dashed2(x) (2.0 * (x) + 1.0)
#define f2(x) (A * (x) / sqrt(1.0 + B * (x) * (x)))
#define f(x) (((x) < C) ? f1(x):f2(x))
#define f_dashed(x) (((x) < C) ? f1_dashed2(x) : f2_dashed2(x))
 

double f2_dashed2(double x)
{
double alpha = sqrt(1.0 + B * x * x);
return( A / (alpha * alpha * alpha) );
}

/* This is the state dynamics.
Inputs :

Output : */
void hillcar_f(task *tsk, double *state, double action, double *f)
{
double u, x, q, p, acc;

x = state[0];
q = f_dashed(x);
p = 1.0 + (q * q);
acc = (action / (MASS * sqrt(p))) - (GRAVITY * q / p);

f[0] = state[1];
f[1] = acc;
}

/* This is the stochastic part.
The stochastic differential equation :
dx = f(x,u) dt + s(x,u) dw
includes 2 part :

Let the matrix a=s.s' (where ' means the transpose)
Then a is a 2x2 symetric positive matrix, thus there exists a set
of 2 orthogonal eigenvectors e1 and e2 with eigenvalues l1 and l2.
This function takes as input : and returns the output : For example,
- if there is no noise (deterministic process) just return l1 = l2 = 0.
*/
void hillcar_noise(task *tsk, double *state, double action,
double *eig_val, double **eig_vect)
{
/* In this example, the noise is constant (does not depend on
the state or the action) and is as follow :
the eigenvalues and the eigenvectors are :
l1= 0.03 for e1=( 1 0 )
l2= 0.3 for e2=( 0 1 )
*/
eig_val[0]=0.03;
eig_val[1]=0.3;

eig_vect[0][0]=1;
eig_vect[1][0]=0;

eig_vect[0][1]=0;
eig_vect[1][1]=1;
}
 

/* The current reinforcement (here 0 everywhere) */
double hillcar_current_reinf(task *tsk, double *state, double action, double seconds)
{
return 0;
}

/* The terminal reinforcement : this function is called only when the systems exits from the state space.

*/
double hillcar_terminal_reinf(task *tsk, double *state)
{
double x=state[0];
double y=state[1];
if (y<0) y=-y;
if (x<0) return -1;
return 1.0- y/2.0;
}
 

Some numerical values :