Variable Resolution Discretization
in Optimal Control (page 2)
Remi
Munos
Andrew Moore
3- Splitting methods based on
local considerations:
-
We start with an initial coarse discretization:

-
At each iteration we split (with some rate) the cells of highest "corner-value
difference". The second discretization is:

-
After 15 iterations, we obtain the following discretization:

Splitting criterion = Value difference
-
where we observe an increase of resolution around the discontinuity of
V and its gradient.
-
The next splitting criterion used is to split whenever the value function
is not linear (instead of not constant). We obtain the following discretization:

Splitting criterion = value non-linearity
-
similar to the previous criterion but refines more parsimoniously.
-
Another difference is the 2 "tails" observed around the discontinuity.
This comes from the fact that the discontinuity is approximated by some
sigmoid function (see below) which is mostly non-linear not at its center
but around it.
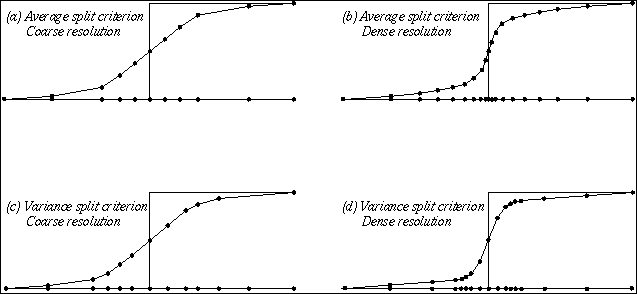
Approximation of a discontinuity with splitting methods based on corner-difference
((a) for a coarse resolution, (b) for a dense resolution) and on value-non-linearity
((c) for a coarse resolution, ((d)) for a dense resolution).
-
However the previous methods spend a lot of ressources on approximating
the discontinuity of V whereas there is no change in the optimal control
in this area!
-
Next idea : split where there is a change in the optimal policy. We obtain
the following discretization:
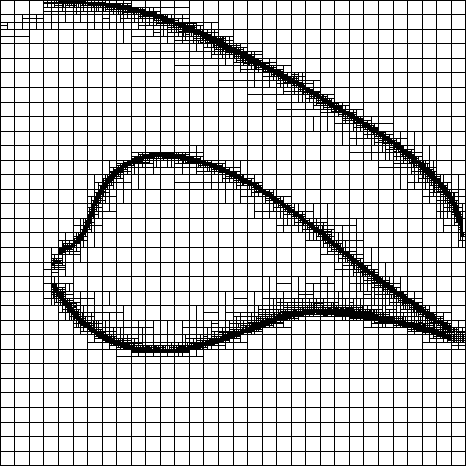
Splitting criterion = policy disagreement
-
However : the control switching boundaries are not optimally located because
the value function is not accurately enough approximated.
-
Next : combination of 2 previous methods in order to approximate both the
value function and the optimal control switching boundaries. We obtain:
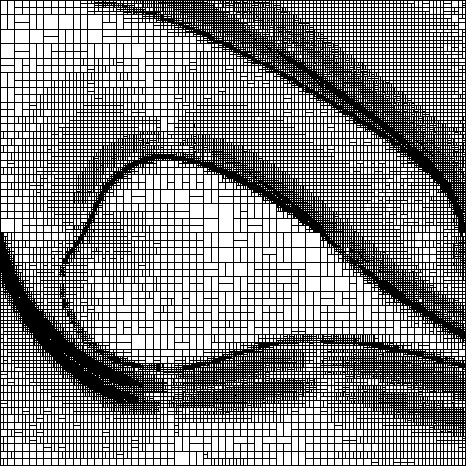
Splitting criterion = combination of policy disagreement and value
non-linearity
-
The problem is that we still spend a lot of ressources to approximate the
value function around the discontinuities.
-
We would like a criterion based on global considerations that would
split only when it is necessary to improve the quality of the controller.
-
Thus we want to define what is the influence of splitting a specific cell
on the whole state space, and see what cells need to be refined in order
to improve the quality of approximation of the value function around the
areas of change in the optimal control (in order to get a good approximation
of the optimal control switching boundaries).









