DIGISLID "DIGItal set-valued and homogeneous SLIding mode control and Differentiators: the implicit approach" (ANR 18 CE40 0008) is a project funded by The French National Research Agency (ANR). The start of the project is October 2018 for a duration of 3 years.
Project Coordinator
Bernard Brogliato
Tel: + 33.(0)4.76.61.53.93
Mail : bernard.brogliato@inria.fr
Scientific Objectives
Sliding-mode controllers (SMC) have been introduced in the former USSR around 1950. Today they are one of the most popular nonlinear feedback controllers (as witnessed for instance by the more than 5000 Google Scholar citations of Prof. Utkin's seminal article at IEEE Transactions on Automatic Control in 1977, a remarkable number for a Control paper). Basically, SMC use switching, or discontinuous functions of the so-called sliding-variable, which is constructed from the system's state and represents the ''output'' to be regulated at zero. The goal is to bring the system's state to the sliding surface in a finite-time and in a robust way in order to create a so-called sliding mode. The essence of SMC is the set-valuedness of the switching control signal, yielding closed-loop systems to be modeled by Differential Inclusions, usually embedded into Filippov's mathematical framework.
SMC are particularly appreciated for their simplicity of tuning and their robustness with respect to large classes of disturbances. However they are also known to suffer from three main issues which are SMC's Achille's heel:
-
the presence of chattering (high frequency oscillations of the output which decreases accuracy, and high frequency bang-bang-like inputs, that may drastically decrease actuators life expectation),
- the need for a precise calculation of the sliding variable (which often depends on the derivatives of a measured noisy signal),
- the sensitivity with respect to neglected dynamics like actuator dynamics (which may create itself chattering).
The implementation of controllers is nowadays most of the time performed with computers. Consequently the analysis of digital SMC is mandatory. It has been shown theoretically by Galias et al (see e.g. [Galias2007, Galias2008]) and experimentally in [Wang2015, Huber2016a, Huber2016b, Huber2016c], that the ''classical'' explicit Euler discretisation creates chattering (the so-called numerical, or digital, chattering). Moreover it may also yield closed-loop instability [Efimov2017, Levant2013]. In other words, the emulation method (the control is first designed and analyzed in continuous-time, then it is discretised with respect to time, and one hopes that the closed-loop behavior and properties are preserved after the discretisation), is not straightforward for set-valued SMC. Especially recovering a good approximation of the continuous-time input (using for instance Filippov's framework for differential inclusions) cannot be done if an explicit Euler method is used for the implementation (in fact, the explicit method produces similar effects to a step motor that switches between two constant values, and it necessarily yields a high-frequency bang-bang signal).
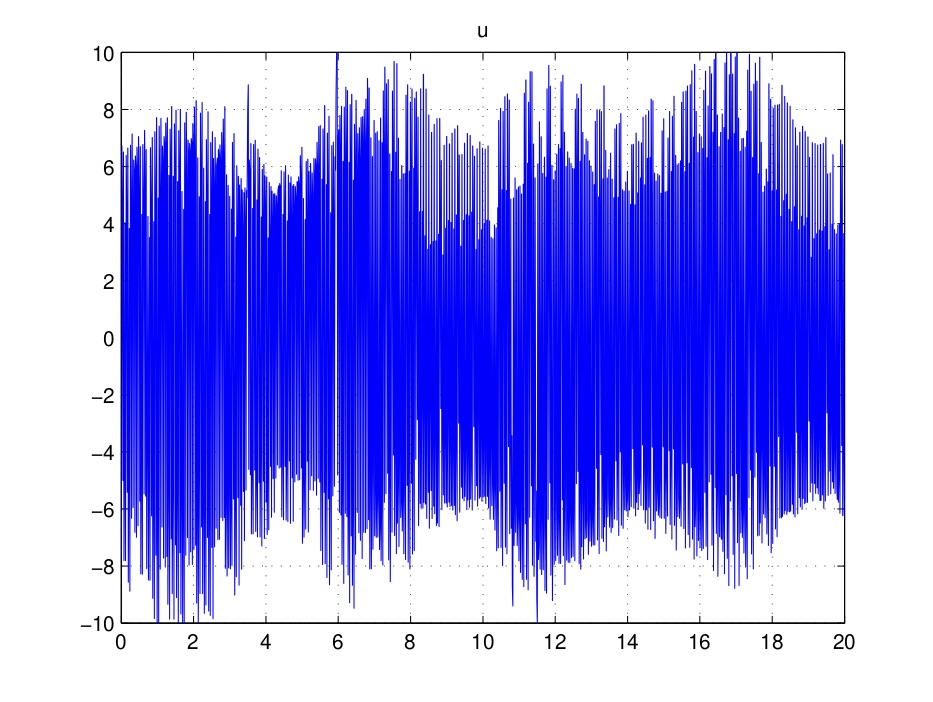
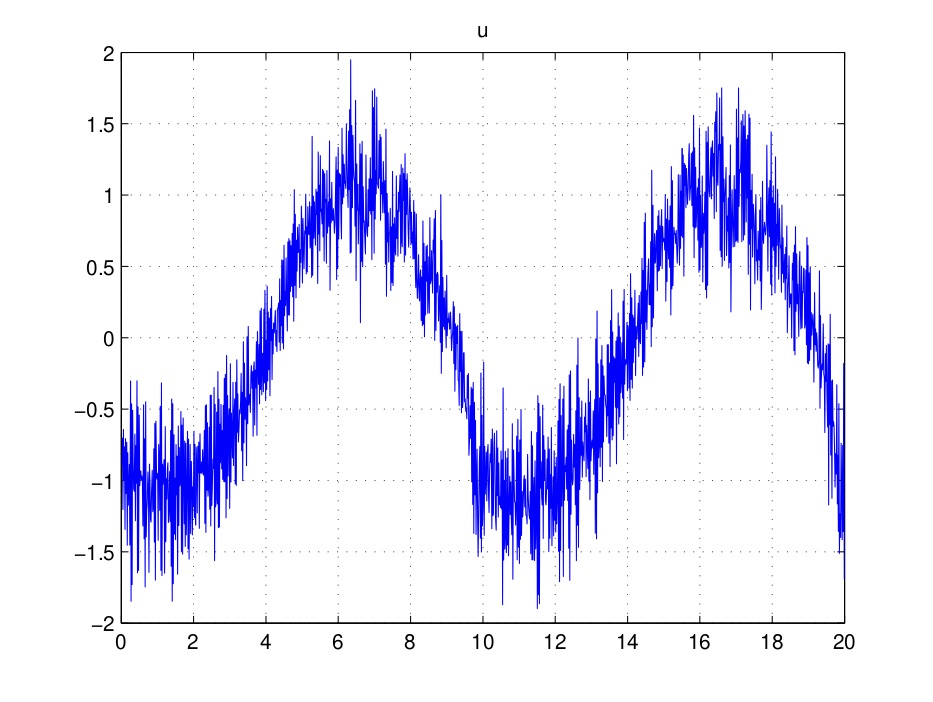
An efficient way to alleviate numerical chattering in both the input and the output (the second point being crucial for applications, though often neglected in the literature), and to guarantee the global finite-time stability, is to replace the explicit Euler discretisation of the set-valued part of the SMC, by the so-called implicit discretisation introduced in [Acary2010] and further investigated theoretically and experimentally in [Acary2016, Efimov2017, Acary2012, Brogliato2015, Miranda2017, Miranda2018, Wang2015, Huber2016a, Huber2016b, Huber2016c, Brogliato2018, Polyakov2018, Xiong2013]. Some experiments led on the electro-pneumatic setup of LS2N (see a description below) are reported in the figure below, showing the significant discrepancy between the explicit (left figure) and the implicit (right figure) inputs for a first-order sliding mode controller: the input magnitude is divided by a factor 3/8, and the chattering is drastically decreased (see [Huber2016c,Wang2015] for more details). See also a
video illustrating the difference between the explicit and the implicit algorithms.
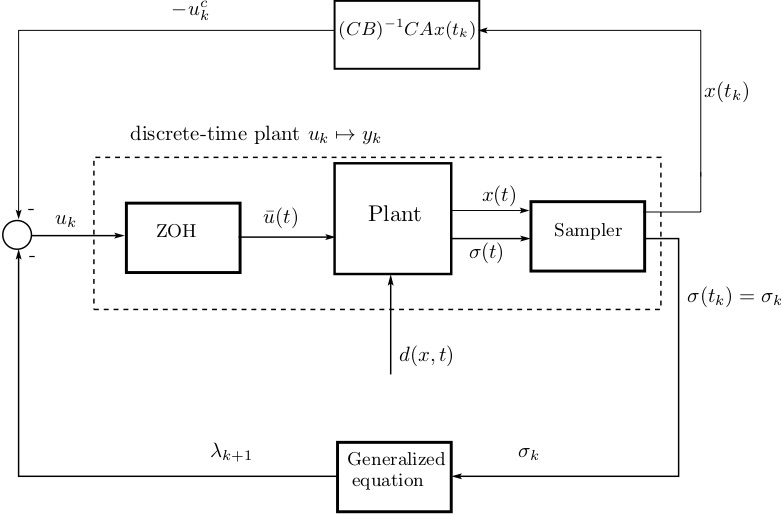
A block-diagram representing the general structure of the implicit discretisation implementation, is given below. It consists of a nominal unperturbed plant that is used to build a generalized equation (which can be a variational inequality, or a complementarity problem, or a simple projection, depending on the type of SMC), whose solution is used to calculate the input u_k to be applied on the interval [t_k, t_k+1]. In the absence of disturbance, both the nominal and the discretised plants are the same.
Bibliography
[Galias2007] Z. Galias, X. Yu, Euler's discretization of single input sliding-mode control systems, IEEE Transactions on Automatic Control, vol.52, no 9, pp.1726-1730, 2007.
[Galias2008] Z. Galias, X. Yu, Analysis of zero-order holder discretization of two-dimensional sliding-mode control systems, IEEE Transactions on Circuits and Systems ? II: Express briefs, vol.55, no 2, pp.1269-1273, 2008.
[Wang2015] B. Wang, B. Brogliato, V. Acary, A. Boubakir, F. Plestan, Experimental comparisons between implicit and explicit implementations of discrete-time sliding mode controllers: towards input and output chattering suppression, IEEE Transactions on Control Systems Technology, vol.23, no 5, pp.2071-2075, 2015.
[Huber2016a] O. Huber, V. Acary, B. Brogliato, Lyapunov stability and performance analysis of the implicit discrete sliding mode control, IEEE Transactions on Automatic Control, vol.61, no 10, pp.3016-3030, October 2016.
[Huber2016b] O. Huber, V. Acary, B. Brogliato, F. Plestan, Implicit discrete-time twisting controller without numerical chattering: analysis and experimental results, Control Engineering Practice, vol.46, pp.129-141, January 2016.
[Huber2016c] O. Huber, B. Brogliato, V. Acary, A. Boubakir, F. Plestan, B. Wang, Experimental results on implicit and explicit time-discretization of equivalent control-based sliding mode control, in {\em Recent Trends in Sliding Mode Control}, L. Fridman, J.P. Barbot, F. Plestan (Eds.), IET Control, Robotics and Sensors Series 102, pp.207-235, 2016.
[Acary2010] V. Acary, B. Brogliato, Implicit Euler numerical scheme and chattering-free implementation of sliding mode systems, Systems and Control Letters, vol.59, pp.284-293, 2010.
[Efimov2017] D. Efimov, A. Polyakov, A. Levant, W. Perruquetti, Realization and discretization of asymptotically stable homogeneous systems, IEEE Transactions on Automatic Control, vol.62, no 11, pp. 5962-5969, 2017.
[Acary2012] V. Acary, B. Brogliato, Y. Orlov, Chattering-free digital sliding-mode control with state observer and disturbance rejection, IEEE Transactions on Automatic Control, vol.57, no 5, pp.1087-1101, May 2012.
[Brogliato2015] B. Brogliato, A. Polyakov, Globally stable implicit Euler time-discretization of a nonlinear single-input sliding-mode control system', Decision and Control (CDC), IEEE 54th Annual Conference on, Osaka, Japan, pp.5426-5431, December 2015.
[Miranda2017] F. Miranda-Villatoro, B. Brogliato, F. Castanos, Multivalued robust tracking control of Lagrange systems: continuous and discrete-time algorithms, IEEE Transactions on Automatic Control, vol.62, no 9, pp.4436-4450, 2017.
[Miranda2018] F. Miranda-Villatoro, B. Brogliato, F. Castanos,Set-valued sliding-mode control of uncertain linear systems: continuous and discret-time analysis, SIAM Journal on Control and Optimization, vol.56, no 3, pp.1756-1793, 2018.
[Brogliato2018] B. Brogliato, A. Polyakov, D. Efimov, The implicit discretization of the super-twisting sliding-mode control algorithm, submitted to the 15th Int. Workshop on Variable Structure Systems, Graz, Austria, 2018.
[Polyakov2018] A.Polyakov, D. Efimov, B. Brogliato, Consistent discretization of finite-time stable homogeneous systems, submitted to the 15th Int. Workshop on Variable Structure Systems, Graz, Austria, 2018.
[Oliveira2017] T.R. Oliveira, A. Estrada, L.M. Fridman, Global and exact HOSM differentiator with dynamic gains for output-feedback sliding mode control, Automatica, vol.81, no 7, pp.156-163, 2017.
[Ghanes2017] M. Ghanes, J-P. Barbot, L. Fridman, A. Levant, A novel differentiator: A compromise between super twisting and linear algorithms, Decision and Control (CDC), IEEE 56th Annual Conference on, Melbourne, Australia, pp. 5415-5419, December 2017.
[Tahoumy2018] E. Tahoumy, M. Ghanes, F. Plestan, J.-P. Barbot, A new controller switching between linear and twisting algorithms, submitted to American Control Conference, Milwaukee, Winconsin, USA, 2018.
[Levant2003] A. Levant, Higher-order sliding modes, differentiation and output-feedback control, International Journal of Control, 76(9-10), pp. 924-941, 2003.
[Polyakov2015] A. Polyakov, D. Efimov, W. Perruquetti, Finite-time and fixed-time stabilization: Implicit Lyapunov function approach, Automatica, vol.51, pp.332-340, 2015.
[Utkin2016] V. Utkin, Discussion aspects of high-order sliding mode control, IEEE Transactions on Automatic Control, vol.61, no 3, pp.829-833, 2016.
[Lopez2018] F. Lopez-Ramirez, A. Polyakov, D. Efimov, W. Perruquetti, Finite-time and fixed-time observer design: Implicit Lyapunov function approach, Automatica, vol.87, pp.52-60, 2018.
[Rosales2013] J.A. Rosales, Y. Shtessel, L. Fridman, Performance margins in conventionnal and second order sliding mode controllers, 52nd IEEE Conf. on Decision and Control, Florence, Italy, pp. 3572-3577,2013.
[Oza2014] H.B. Oza, Y.V. Orlov, S.K. Spurgeon, Y. Aoustin, C. Chevallereau, Continuous second order sliding mode based robust finite time tracking of a fully actuated biped robot, European Control Conference, Strasbourg, France, pp. 2600-2605, June 2014.
[Sinclair2014] S. Sinclair, M.M. Wanderley, V. Hayward, Velocity estimation algorithms for audio-haptic simulations involving stick-slip, IEEE Transactions on Haptics, vol.7, no 4, pp.533-544, 2014.
[Aung2018] M.T.S. Aung, Z. Shi, R. Kikuuwe, A new parabolic sliding mode filter augmented by a linear low-pass filter andits application to position control, ASME Journal of Dynamic Systems, measurement, and Control, vol.140, 041005, April 2018.
[Xiong2013] X. Xiong, R. Kikuuwe, M. Yamamoto, Backward-Euler discretization of second order sliding mode control and super-twisting observer for accurate position control, Proceedings ASME 2013 Dynamic Systems and Control Conference, October 2013, Palo Alto, California, USA, DSCC2013-3872.[Levant2013] A. Levant, On fixed and finite-time stability in sliding mode control, 52nd IEEE Int. Conference on Decision and Control, Firenze, Italy, pp.4260-4265, 2013.




