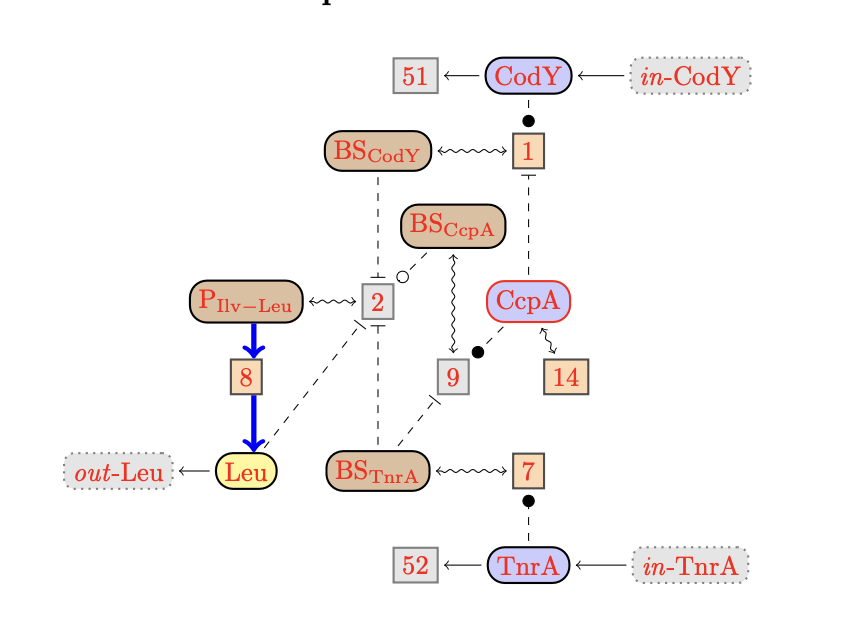
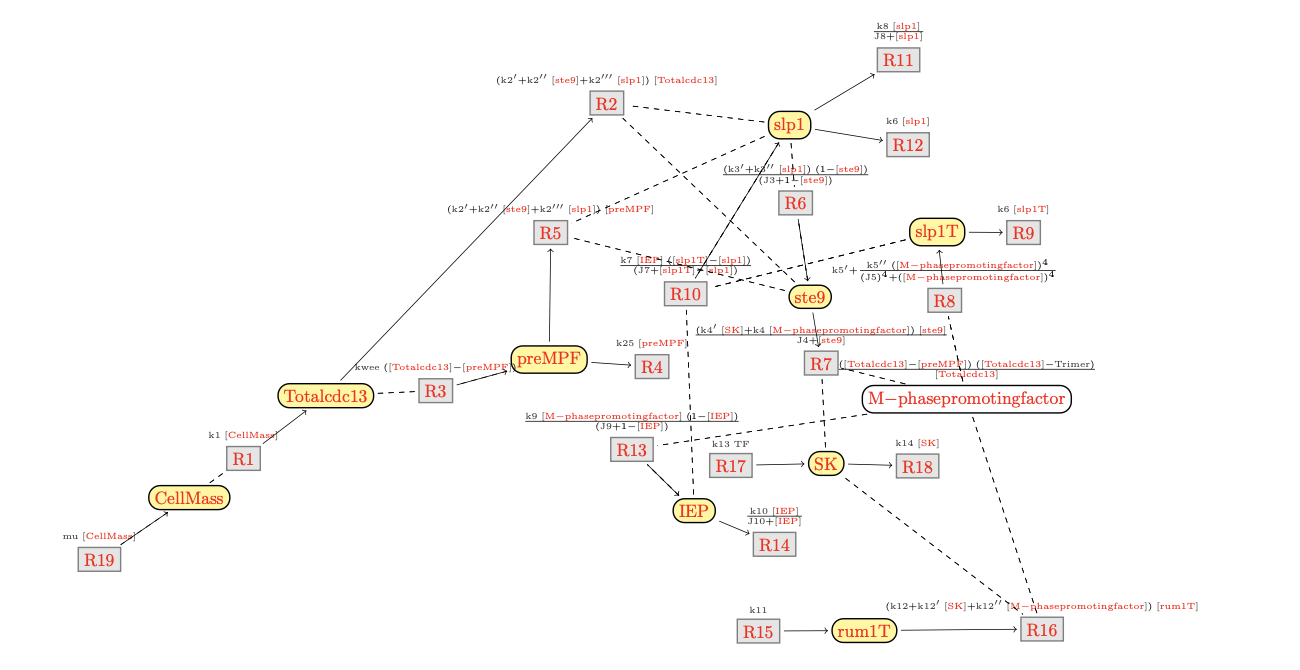
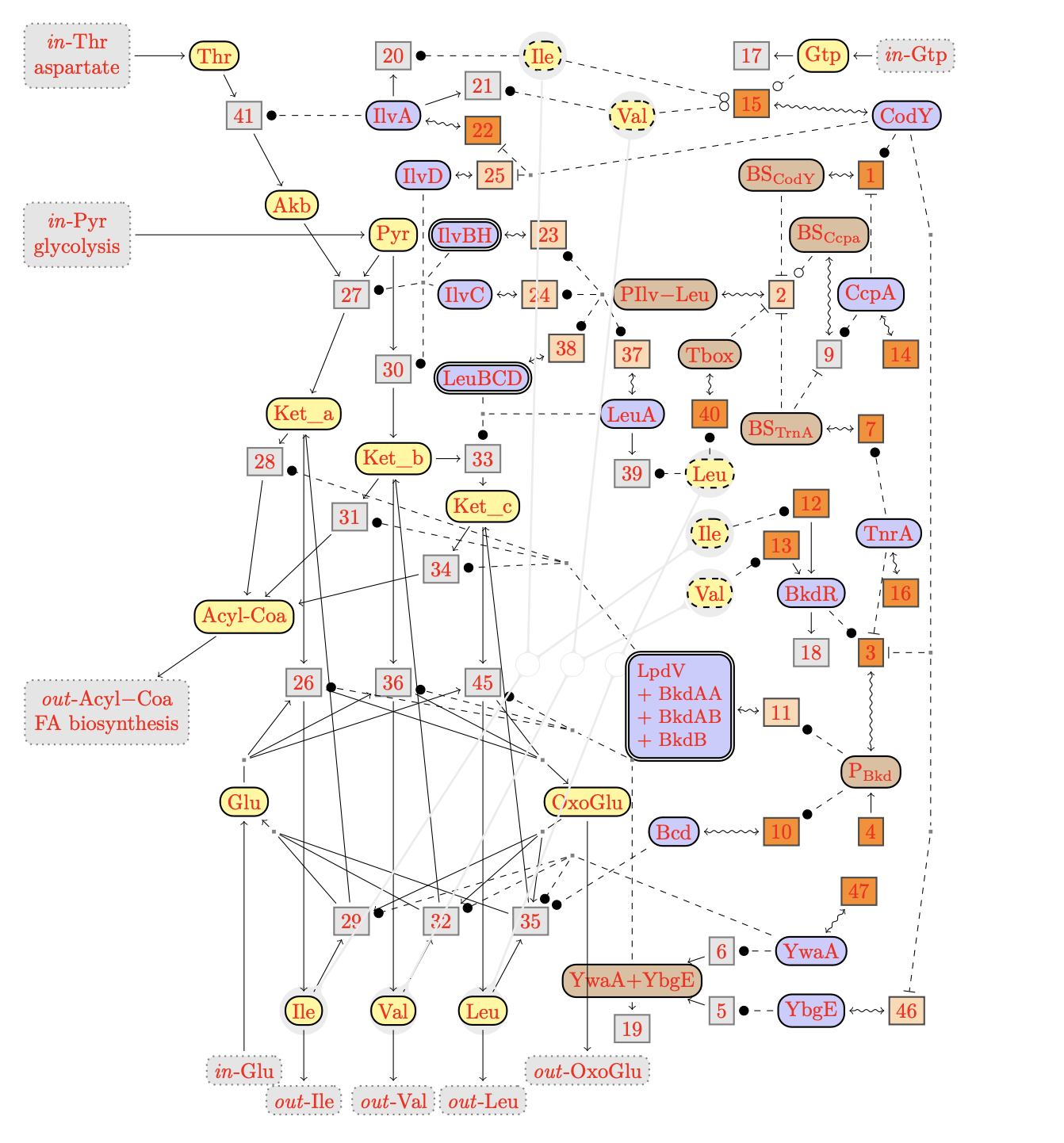
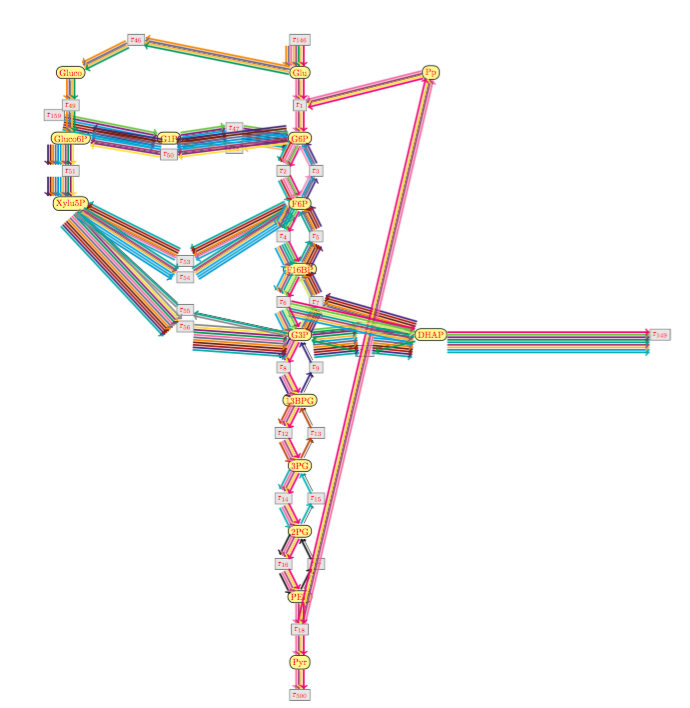
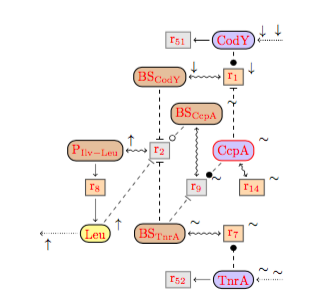
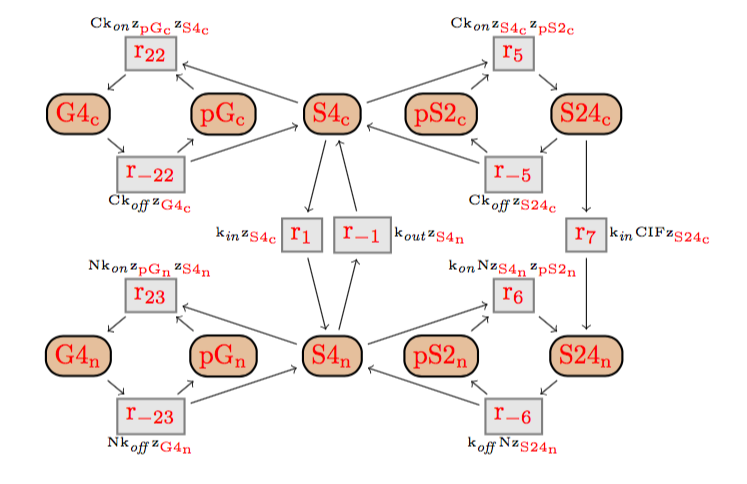
The DTD of BioComputing's reaction networks got generated from its
documentation in the file network-dtd.xml. Please don't
change the generated file network-1.2.dtd manually.
Instead change network-dtd.xml and generate
network-1.2.dtd with the command make network.dtd.
Reactions may either have partial kinetic information given by
modifiers of different types (activator, inhibitor, etc) or
have complete kinetic information given by some kinetic law, i.e.
some arthmetic expression.
A reaction network may contains four kinds of species elements:
(algebraic or differential) species, metabolites, proteins, and
actors.
<!ENTITY % species-elements "
species
| metabolite
| protein
| actor ">
Beside of the set of species elements, a network
contains a set of edge clusters refering
to species elements, reactions, context inflows and outflows,
macros for expressions, definitions of functions,
(control) parameters, and events.
<!ELEMENT network (( comment
| %species-elements;
| reaction
| context
| edgecluster
| expression
| function
| parameter
| event )*) >
A network may have an identfier with a latex-look, a kind, and a
scale for its graph, a name, a source, and a network-version.
<!ATTLIST network
id CDATA #IMPLIED
latex-look CDATA #IMPLIED
kind CDATA #IMPLIED
scale CDATA #IMPLIED
name CDATA #IMPLIED
source CDATA #IMPLIED
network-version CDATA #IMPLIED>
@id:
the identifier is relevant when referening to the networks entities withing
latex[tikz],
@scale:
the scale is a positive real number that permits to scale the x-axis
and y-axis simultaneously,
@kind:
is an identifier which serves for debugging purposes.
The graph of the network contains various kinds of nodes that
must have an identifier.
<!ENTITY % node "
id CDATA #REQUIRED
latex-look CDATA #IMPLIED
x CDATA #IMPLIED
y CDATA #IMPLIED
initial CDATA #IMPLIED
initial-expression CDATA #IMPLIED
comment CDATA #IMPLIED
aux CDATA #IMPLIED
epsilon CDATA #IMPLIED
">
Nodes have the follwoing attributes (where x-axis and y-axis
should be given):
@id:
identifier,
@latex-look:
latex display of the species' id
@x:
coordinate of x-axis,
@y:
coordinate of y-axis,
@initial:
an initial value for time point zero
@initial-expression:
the identifier of some expression macro. This serves for defining the
initial value of a species in dependence from the initial values of
other species
@comment:
a latex comment.
@aux:
epsilon:
Constraints:
- the value of
@x must be castable to xs:float
- the value of
@y must be castable to
xs:float
-
@initial and @initial-expression cannot coexist a the same time.
- The value of
@initial-expression must be the @id
of some macro expression that
is defined in a non-cyclic manner, so that it can be evaluated
to a number at initial time point 0.
Mapping Species Elements to Graph Elements
Each species element is mapped to a node in the graph.
The node of a species element is drawn as circle with solid lines.
A species element may be related to an expression for its compartment size
and for its concentration.
<!ENTITY % species " %node;
compartment CDATA #IMPLIED
concentration CDATA #IMPLIED
essential CDATA #IMPLIED
initialConcentration CDATA #IMPLIED
">
These optional attributes of species have the following meaning:
@compartment:
a species may live in some compartment.
The value of @compartment is then
the @idof some expression macro, which specifies
the compartment's size.
@concentration:
a species may have a concentration besize of
its amount. The value of @concentration
is the "@id" of the expression macro for its concentration.
@essential:
if present, the circle around the species' node will be drawn in red.
It indicates that the presence of the species is
essential for a network to work properly.
@initialConcentration:
Depricated. Use @initial" or
@initial-expression" for the inital
value (amout) of the species instead.
Each species element may have a set of copy nodes, which are drawn as
dashed circles. All nodes for the same species are linked by a splitpoint,
which also is drawn as a node.
Logically, it doesn't matter whether a species participates in a
reaction or one of its copies.
<!ENTITY % copies "((copy+,splitpoint,comment?)?,comment*)">
<!ELEMENT metabolite %copies; >
<!ATTLIST metabolite %species; >
<!ELEMENT protein %copies;>
<!ATTLIST protein %species;
cluster CDATA #IMPLIED >
<!ELEMENT actor %copies; >
<!ATTLIST actor %species; >
<!ELEMENT species ((kinetic-expression)?,(%copies;),(modifier)*) >
<!ATTLIST species %species;
type CDATA #REQUIRED>
Proteins may may represent clusters of proteins in
reality. Whether this is the case, can be indicated by the presence
attribute cluster". In this case the speciess node is drawn with a
double-circle:
@cluster:
the presence of this attribute indicates a protein cluster, its value is
irrelevant.
<!ELEMENT copy (#PCDATA) >
<!ATTLIST copy %node; >
<!ELEMENT splitpoint (#PCDATA) >
<!ATTLIST splitpoint
x CDATA #IMPLIED
y CDATA #IMPLIED
comment CDATA #IMPLIED >
Multiple edges of the network may be clustered for nicer graph presentation.
An edge cluster is represented by a node of the graph, which can be
used everywhere in the same way as a species node can be used.
<!ELEMENT edgecluster (source*)>
A source of an edgecluster is a species, a
copy of species, or an edgecluster that has an outgoing edge
pointing to it.
edgecluster:
a node that clusters edges from serveral sources.
<!ATTLIST edgecluster %node;
type CDATA #REQUIRED>
The type of an edge cluster is the type of edges that point to it. Only edges of
the same type can be clustered.
type:
the value is this element one of the 6 types
of reaction complements (see the entity complement below).
Each source of an edgecluster must contain a reference
to a species
<!ENTITY % species-reference "
spec CDATA #IMPLIED
copy CDATA #IMPLIED
edgecluster CDATA #IMPLIED" >
The combined values of these three attributes must give reference to one or many species:
@spec:
identfier of a species,
@copy:
identifier of a copy of that species,
@edgecluster:
reference to one species or many of them.
Constraints:
-
Either
@spec or @edgecluster must be present,
-
the attribute
@copy is optional in the case where @spec is present.
- in this case, there must be some species
$species with
$species/@id=@spec and $species/copy/@id=@copy.
<!ELEMENT source (#PCDATA) >
<!ATTLIST source %species-reference; >
A reaction network may have are three kinds of reactions, represented
by the following elements:
reaction:
an (internal) reaction,
context[input]:
an inflow from the context,
context[output]:
an outflow to the context.
A (internal) reaction may have various the four kinds of
modifiers given by the following elements:
<!ENTITY % modifier "
modifier
| inhibitor
| activator
| accelerator">
modifier:
a generic modifier
accelerator:
an accelerator speeds up the reaction,
activator:
an activator is an accelerator nececessary to apply the reaction,
inhibitor:
an inhibitor slows down the reaction
A reaction may have three other complements beside modifers:
<!ENTITY % complement "
%modifier;
| reactant
| product
| product-inh">
product:
a product of a reaction,
reactant:
a reactant of a reaction,
product-inh:
a product with an implicit degradation reaction.
A reaction may have a kinetic-expression
which is an arithmetic expression, or a more informal
kinetics, beside of a set of complements.
<!ELEMENT reaction ((comment)*,((kinetics)|(kinetic-expression))?,(expression|%complement;)*) >
Whether a reaction may either be a candidate for knockout
or not can be be specified within the network or externally.
Graphically, reactions are drawn as boxed node. The fill-color of the
box indicates whether the reaction is a candidate for knockout. The nodes
of knockout candidates will be distinguished by a light orange color, while
the others will be clored in gray.
<!ATTLIST reaction %node;
outflow CDATA #IMPLIED
candidate CDATA #IMPLIED >
candidate:
if the attribute is present, the reaction is a candidate for knockout.
A species may interact in with the context
via inflows and outflows.
<!ELEMENT context (input | output)>
<!ATTLIST context %node; >
The two possible context elements are as follows:
context/input:
an inflow from the context,
The second form is depricated since replace by reactions with
@outflow attribute:
context/output:
an outflow into the context,
The value of attribute spec of a context inflow or outflow is
the identifier of the interacting species:
<!ENTITY % species-identifier "
spec CDATA #REQUIRED
copy CDATA #IMPLIED " >
<!ELEMENT input (#PCDATA)>
<!ATTLIST input %species-identifier; >
<!ELEMENT output (#PCDATA)>
<!ATTLIST output %species-identifier; >
Comments are given in latex format:
<!ELEMENT comment (#PCDATA)>
<!ATTLIST comment
latex CDATA #IMPLIED
experiment CDATA #IMPLIED
prediction CDATA #IMPLIED >
References to real numbers (or real functions) are
given by the following elements.
There are constant, variables
var, reference to control parameters param, references to
the value of species conc either concentrations of amounts,
references to the value of expression macros expr,
and references to the speed of a reaction,
i.e. to its kinetic-expression
<!ENTITY % reference "constant | param | conc | speed | var | expr ">
<!ELEMENT constant (#PCDATA)>
<!ATTLIST constant
id CDATA #IMPLIED
value CDATA #IMPLIED >
<!ELEMENT param (#PCDATA)>
<!ATTLIST param
id CDATA #REQUIRED >
<!ELEMENT expr (#PCDATA) >
<!ATTLIST expr
id CDATA #REQUIRED >
<!ELEMENT var (#PCDATA)>
<!ATTLIST var
id CDATA #IMPLIED >
<!ELEMENT conc (#PCDATA)>
<!ATTLIST conc
spec CDATA #REQUIRED >
<!ELEMENT speed (#PCDATA)>
<!ATTLIST speed
reaction CDATA #REQUIRED >
An arithmetic expression sometimes defines a real number in
the simplest case. But in most cases, they define real-valued
function.
The atomic expressions are the references above. There are
applications of buildin arithmetic functions mult,
power, etc.
The buildin functions are named as usual
in MathML However, they are applied with a
simplified syntax compared to MathML without
using any apply elements.
<!ENTITY % expression "
%reference; |
mult|sum|divide|minus|
sin|cos|tan|cot|
sinh|cosh| tanh| coth|
floor| ceiling|
log| power|
time | inh | delay|
ifthenelse |
apply ">
<!ELEMENT mult (%expression;)*>
<!ELEMENT sum (%expression;)*>
<!ELEMENT divide ((%expression;),(%expression;))>
<!ELEMENT minus ((%expression;),(%expression;)?)>
<!ELEMENT power ((%expression;),(%expression;))>
<!ELEMENT log ((%expression;), (%expression;))>
<!ELEMENT sin (%expression;)>
<!ELEMENT cos (%expression;)>
<!ELEMENT tan (%expression;)>
<!ELEMENT cot (%expression;)>
<!ELEMENT sinh (%expression;)>
<!ELEMENT cosh (%expression;)>
<!ELEMENT tanh (%expression;)>
<!ELEMENT coth (%expression;)>
<!ELEMENT ceiling (%expression;)>
<!ELEMENT floor ((%expression;))>
Beside of the usual building operators from MathML, there
are the following more specific operators:
-
time for the identity function
-
inh for the inhibition function
with inh(x)=1/1+x
-
delay for delays in differential equations
-
ifthenelse for conditionals
-
apply for applying function defined in the network
itself (rather than being buildin in MathML).
<!ELEMENT time (#PCDATA)>
<!ELEMENT delay ((%expression;), (%expression;))>
<!ELEMENT inh (%expression;)>
<!ELEMENT apply ((%expression;)*)>
<!ATTLIST apply
fun CDATA #REQUIRED
latex-look CDATA #IMPLIED >
Arithmetic expressions subsume conditionals ifthenelse
that permit to define piecewise functions. They contain boolean
expressions as conditions, which may compare
real numbers for equality or ordering. Furthermore,
Boolean expressions are closed under the boolean operators.
<!ENTITY % boolexpression "eq | lt | leq | and | or | not">
<!ELEMENT ifthenelse
((%boolexpression;),(%expression;),(%expression;))>
Functions can be defined by using lambda expressions
possibly binding several variables at once.
<!ELEMENT function (lambda)>
<!ATTLIST function %node;>
<!ELEMENT lambda ((bvar | %expression;)*)>
<!ELEMENT bvar (#PCDATA)>
<!ATTLIST bvar
id CDATA #IMPLIED >
A reaction may have a kinitic law that is described by the element
kinetic-expression and defined by some artihmetic expression:
<!ELEMENT kinetic-expression (%expression;)>
<!ATTLIST kinetic-expression
angle CDATA #IMPLIED >
A way to describe kinetics in a partial manner is by using the
element kinetics instead of
kinetic-expression. This method is depricated.
Named kinetics such as mass-action can be defined by arithmetic
functions instead.
<!ELEMENT kinetics (#PCDATA) >
<!ATTLIST kinetics
id CDATA #IMPLIED
expr CDATA #IMPLIED
mode CDATA #IMPLIED
angle CDATA #IMPLIED >
The kinetics is described either by the identifier @id or
informally by the latex expression @expr. Whether the
descriptor is exact or up to similarity is specifie by @mode.
@id:
An identfier of a kinetics, which must have either of the following three values
-
exp : expression kinetics with constant equal to 1
-
ma : mass action kinetics with rate constant equal to 1
-
deac: deactivation kinetics with rate constant equal to 1
@expr:
an arbitrary latex expression describing the kinetics.
It may use the following predefined latex macros:
-
\BS{...} for binding sites,
-
\Prom{...} for promoters, and
-
\Op{...} for operons.
Other latex macros can be user defined by addition to the file
Graph/Latex/macros.sty.
@mode:
The interpretation mode may be either modulo similarity or exact. In the
former case, the attribute mode must be absent, in the latter it must
satisfy mode="equal".
@angle:
The attribute angle says where the descriptor of the kinetics is annotated at
the reaction node. If the id attribute is present, then the value of
the annotation is the value of attribute expr.
Constraints:
- exactely one of the attributes
@id and @expr must be present.
- the only possible value for
@mode is equal.
- the only possible values for
@id are exp,
ma, and deac
Modifiers and Reaction Complements
Reactions may have four kinds of modfiers:
genral modifiers, inhibitors, activators, accelerators.
<!ELEMENT modifier (#PCDATA) >
<!ATTLIST modifier %species-reference; >
<!ELEMENT inhibitor (#PCDATA) >
<!ATTLIST inhibitor %species-reference; >
<!ELEMENT activator (#PCDATA) >
<!ATTLIST activator %species-reference; >
<!ELEMENT accelerator (#PCDATA) >
<!ATTLIST accelerator %species-reference; >
Beside of the modifiers there are three other kinds of reaction complements:
reactants, products, and inhibited products (hiding a degradation reaction).
<!ENTITY % reaction-complement "%species-reference;
stoichiometry CDATA #IMPLIED" >
<!ELEMENT reactant (#PCDATA) >
<!ATTLIST reactant %reaction-complement; >
<!ELEMENT product (#PCDATA) >
<!ATTLIST product %reaction-complement; >
<!ELEMENT product-inh (#PCDATA) >
<!ATTLIST product-inh %reaction-complement; >
@stoichiometry:
the value of the stoichiometry attribute it is computed automatically by the implementation.
User defined stoichiometry values will be overwritten so that they become correct if necessary.
We also have expressions defined by macros. These
can be refered to by using the tag expr.
<!ELEMENT expression (%expression;)>
<!ATTLIST expression %node; >
Control Parameters and Events
A control parameter defines a trajectory by some arithmetic expression
<!ELEMENT parameter (#PCDATA)>
<!ATTLIST parameter %node; >
An event has a triger condition and a set of updates
<!ELEMENT event (condition, (update)*)>
<!ATTLIST event
id CDATA #IMPLIED >
An trigger condition is a conjunction of equations and inequations
<!ELEMENT condition (%boolexpression;)>
<!ELEMENT eq ((%expression;),(%expression;))>
<!ELEMENT lt ((%expression;),(%expression;))>
<!ELEMENT leq ((%expression;),(%expression;))>
<!ELEMENT and ((%boolexpression;)*)>
<!ELEMENT or ((%boolexpression;)*)>
<!ELEMENT not (%boolexpression;)>
we can update the concentrations of species and the values of parameters
<!ELEMENT update ((conc|param), (%expression;))>
<!ATTLIST update>