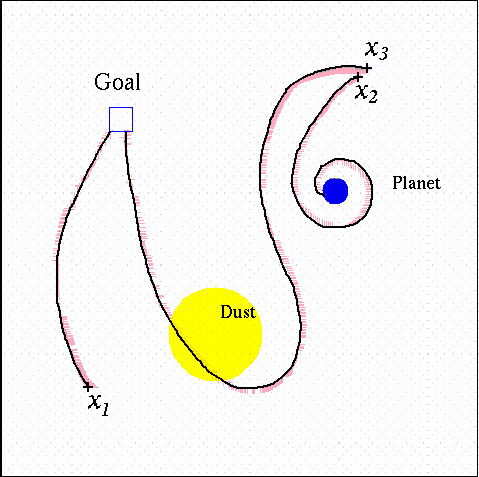

The state space :
The space-shuttle problem is defined by the 4-dimensional state x=(x1, x2, x1_dot, x2_dot)The control space :
where (x1, x2) are the coordinates of the space-shuttle and (x1_dot, x2_dot) their velocities.
The control u takes 5 possible values corresponding to :The state dynamics :
- u = 0 means no thrust
- u = 1 means thrust to the right
- u = 2 means thrust to the left
- u = 3 means thrust to the top
- u = 4 means thrust to the bottom
The state dynamics is defined by the differential equation :The reinforcement functions :
dx
-- = f(x,u)
dt
in the deterministic case, and by the stochastic diff. eq. :dx = f(x,u) dt + s(x,u) dw
in the stochastic case. Here dw is a Wiener process.
(The formulation of the stochasticity is explained is the
function space_noise).
The current and terminal reinforcement functions are describedCode in C :
in the functions :
- space_current_reinf
- space_terminal_reinf
/* Definition of some constants */
#define GRAVITY 9.81
#define m 0.1 /* mass of the space shuttle */
#define M1 2 /* mass of planet 1 */
#define R1 0.6 /* radius of planet 1 */
#define X1 4.0 /* coordinates of planet 1 */
#define Y1 2.0
#define M2 1.5 /* mass of planet 2 */
#define R2 2 /* radius of planet 2 */
#define X2 -1.0 /* coordinates of planet 2 */
#define Y2 -4.0
#define Gx -5 /* coordinates of the Goal */
#define Gy 5
/* This is the state dynamics.
Inputs :
double k=0.08;
double x=state[0];
double y=state[1];
double vx=state[2];
double vy=state[3];
double a_to_ax[5] = {0, 1, -1, 0, 0};
double a_to_ay[5] = {0, 0, 0, 1, -1};
double ax=a_to_ax[action];
double ay=a_to_ay[action];
double fx, fy;
double dx1=(X1-x), dy1=(Y1-y);
double dx2=(X2-x), dy2=(Y2-y);
double d1,d2;
d1=sqrt(dx1*dx1+dy1*dy1);
d1=d1*d1*d1;
d2=sqrt(dx2*dx2+dy2*dy2);
if (d2 > R2) d2=d2*d2*d2;
else d2=R2*R2*R2;
fx = GRAVITY * m * (M1 * dx1 / d1 + M2 * dx2 / d2);
fy = GRAVITY * m * (M1 * dy1 / d1 + M2 * dy2 / d2);
f[0]=vx;
f[1]=vy;
f[2]=fx + k*ax;
f[3]=fy + k*ay;
}
/* This is the stochastic part.
The stochastic differential equation :
dx = f(x,u) dt + s(x,u) dw
includes 2 part :
eig_vect[0][0]=1;
eig_vect[1][0]=0;
eig_vect[2][0]=0;
eig_vect[3][0]=0;
eig_vect[0][1]=0;
eig_vect[1][1]=1;
eig_vect[2][1]=0;
eig_vect[3][1]=0;
eig_vect[0][2]=0;
eig_vect[1][2]=0;
eig_vect[2][2]=1;
eig_vect[3][2]=0;
eig_vect[0][3]=0;
eig_vect[1][3]=0;
eig_vect[2][3]=0;
eig_vect[3][3]=1;
}
/* The current reinforcement penalizes
the consumption of fuel (action != 0) */
double space_current_reinf(task *tsk,
double *state, double action, double seconds)
{
double cost;
if (action > 0) cost += 0.01 * seconds;
return -cost;
}
/* The terminal reinforcement :
If the systems has reached
the goal then R=+10, otherwise (R=-10) if the space-shuttle touches the
planet1 or exits from the state space.
*/
double space_terminal_reinf(task *tsk,
double *state)
{
if (in_goal(tsk, state)) return 10.0;
else return -10.0;
}
Some numerical values :