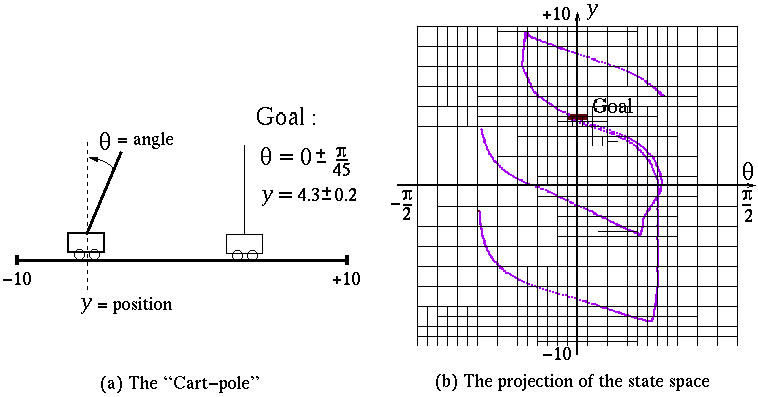

The state space :
The Cartpole is defined by the 4-dimensional state x=(theta, y, theta_dot, y_dot)The control space :
where theta is the the angles of the pole, y the position of the cart (see figure) and (theta_dot, y_dot) are their respective velocities.
The control u is a 1-dimensional variable that takes aThe state dynamics :
finite number of possible values between -max_u and +max_u.
It represents the thrust applied to the cart.
The state dynamics is defined by the differential equation :The reinforcement functions :
dx
-- = f(x,u)
dt
in the deterministic case, and by the stochastic diff. eq. :dx = f(x,u) dt + s(x,u) dw
in the stochastic case. Here dw is a Wiener process.
(The formulation of the stochasticity is explained is the
function Cartpole_noise).
The current and terminal reinforcement functions are describedCode in C :
in the functions :
- Cartpole_current_reinf
- Cartpole_terminal_reinf
/* Definition of some constants and basic functions
*/
#define CART_MASS 1.0
#define POLE_MASS 0.1
#define POLE_LENGTH 1.0
/* This is the state dynamics.
Inputs :
theta = state[0];
theta_dot = state[2];
u = action;
theta_double_dot = (((CART_MASS + POLE_MASS) * 9.8 * sin(theta)
-
(u + POLE_MASS
* POLE_LENGTH * theta_dot * sin(theta))*cos(theta)) /
((4.0 / 3.0) * (CART_MASS
+ POLE_MASS) * POLE_LENGTH -
(POLE_MASS *
POLE_LENGTH * pow(cos(theta), 2))));
x_double_dot = ((pow(theta_dot, 2) * sin(theta) - theta_double_dot
*sin(theta))
* POLE_MASS * POLE_LENGTH
+ u) / (POLE_MASS + CART_MASS);
f[0]=theta_dot;
f[1]=state[3];
f[2]=theta_double_dot;
f[3]=x_double_dot;
}
/* This is the stochastic part.
The stochastic differential equation :
dx = f(x,u) dt + s(x,u) dw
includes 2 part :
eig_vect[0][0]=1;
eig_vect[1][0]=0;
eig_vect[2][0]=0;
eig_vect[3][0]=0;
eig_vect[0][1]=0;
eig_vect[1][1]=1;
eig_vect[2][1]=0;
eig_vect[3][1]=0;
eig_vect[0][2]=0;
eig_vect[1][2]=0;
eig_vect[2][2]=1;
eig_vect[3][2]=0;
eig_vect[0][3]=0;
eig_vect[1][3]=0;
eig_vect[2][3]=0;
eig_vect[3][3]=1;
}
/* The current reinforcement (here 0 everywhere)
*/
double Cartpole_current_reinf(task *tsk,
double *state, double action, double seconds)
{
return 0;
}
/* The terminal reinforcement : this function
is called only when the systems exits from the state space.
If the systems has reached
the goal then R=+1, otherwise R=-1.
*/
double Cartpole_terminal_reinf(task *tsk,
double *state)
{
if (in_goal(tsk, state) return 1.0;
else return -1.0;
}
Some numerical values :